Physics Practical Skills Part 4: Drawing graphs and lines of best fit

In part 4 of the Physics Skills Guide, we explain how to draw a line of best fit correctly in Physics Practicals. Read the post to learn about dos and don'ts of drawing a line of best fit.
guide-physics-practical-guide-how-to-draw-a-line-of-best-fit-banner.

Introduction to Drawing Graphs and Lines of Best Fit

In this Guide, we explain the importance of scientific graphs in Physics and how to draw scientific graphs correctly including lines of best fit. This is a really important Physics skill and you’ll need to master it if you want to ace your next Physics Practical exam.

 

In this article we discuss:

 

Want to ace your next Physics Practical Assessment?

Learn how to:

  • Assess the validity, reliability and accuracy of any measurements and calculations
  • Determine the sources of systematic and random errors
  • Identify and apply appropriate mathematical formulae and concepts
  • Draw appropriate graphs to convey relationships

with the Matrix Practical Skills Workbook.

Sharpen your Physics skills

Get exam-ready for your Physics practical assessments with this FREE practical skills workbook.

Download now

Scientific Graphs

What are scientific graphs?

A graph is a visual representation of a relationship between two variables, x (the independent variable) and y (the dependent variable).

Graphs make it easy to identify trends in data that you have collected and can be analysed in order to perform a calculation or a measurement, related to addressing the aim of an experiment.

How to draw a scientific graph

StepActionDetail
1Identify the variables
  • Place your independent variable on the x-axis of your graph and the dependent variable on the y-axis.
2Determine the variable range
  • Subtract the lowest data value from the highest data value
3Determine the scale of the graph
  • Determine a scale, (the numerical value for each square or division), that best fits the range of each variable.
  • Use a scale that allows your data to be graphed as large as possible in the space provided.
  • The range of each axis may be different. They do not need to start at zero but it is recommended as this allows you to extrapolate if needed.
  • The scale of each axis may be different, but each one must be consistent. If one division represents one metre at the beginning of the graph on one axis, one division always represents one metre on that axis.
4Number and label each axis
  • Clearly label the x and y-axes including the units of each measurement.
5Plot the data points
  • Plot each data value on the graph with a cross (x)
6Draw the graph
  • Identify a trend or a relationship between the independent and dependent variables.
  • Remove any outliers from consideration.
  • Draw a curve or a line that best describes the identified trend. Most graphs of experimental data in Physics are linear and not drawn as “connect­ the ­dots”.
  • Only draw the line (or curve) over the range for which you have data. Do not extend your line beyond this range.
  • If required to extrapolate (extend the graph along the same slope beyond the range of data), use a dotted line to indicate that you are extrapolating.
7Provide a descriptive title
  • Your title should clearly communicate what the graph is about. Do not simply restate what is already shown on the axes.

In Year 11 and 12 Physics, the trends that you will investigate are mostly linear, or can be converted into linear graphs, and, hence, you’ll be required to draw a line of best fit.

 

Drawing the line of best fit

An example of a correctly drawn line of best fit is shown below, along with an incorrect one:

How to draw a line of best fit

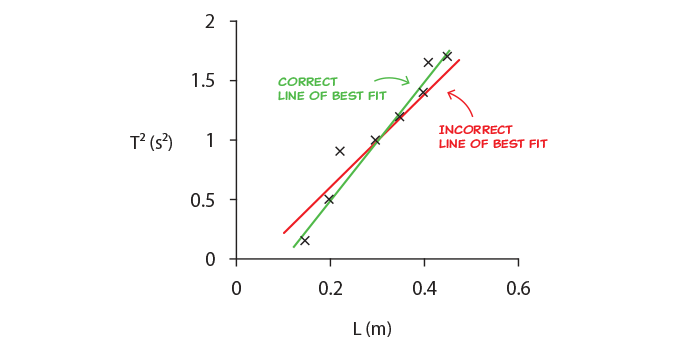
To draw the line of best fit, consider the following:

  • Outliers must be ignored.
  • The line must reflect the trend in the data, i.e. it must line up best with the majority of the data, and less with data points that differ from the majority.

 

  • The line must be balanced, i.e. it should have points above and below the line at both ends of the line.

  • DO NOT force the line to pass through any specific data points, or to pass through zero. The purpose of the line of best fit is to reveal the trend of all the data.

Why do we need to draw a line of best fit?

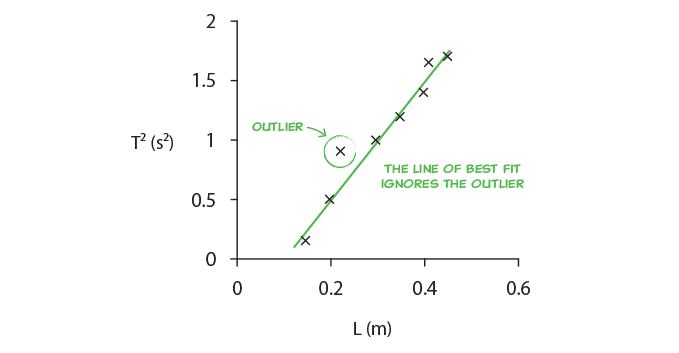
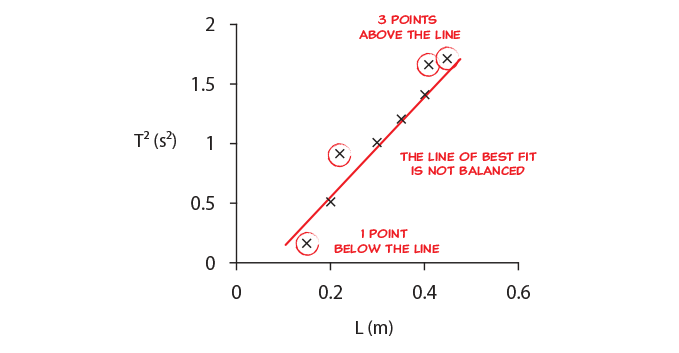
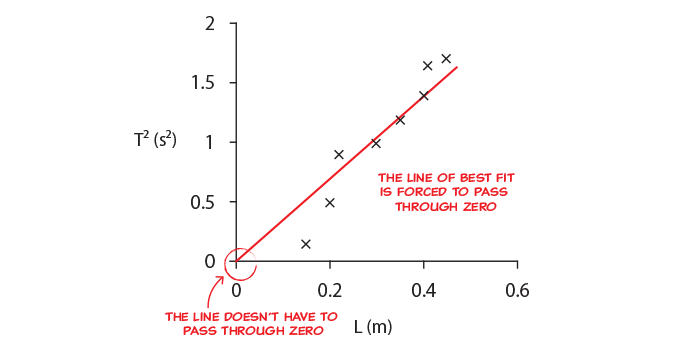
The main reasons for drawing a line of best fit are to:

  • Reduce the effect of both systematic and random error and thus make the experiment more accurate and more reliable.
  • Find and use the gradient of the line of best fit to determine an unknown in the experiment. Usually determining this unknown addresses the aim in some way

How does the line of best fit reduce experimental errors?

By drawing the line of best fit we are looking for the strongest trend in the data, and in this way reduce the effect of random errors. If we then use the gradient of the line of best fit we look at differences in values rather than absolute values, which reduces or eliminates the effect of systematic errors.

The graphs below illustrate four examples with different types of errors and with no errors:

  1. Perfect data with no errors
  2. Random error
  3. Random error with outlier
  4. Random and systematic errors

The gradient represents the result of the experiment and should have a value of 1, so the equation of the line is \(y=x\).

guide physics how to draw line of best fit lines of best fit to different types of errors

How does using a line of best fit reduce experimental errors?

Using a graph gives results that are as good or better than calculating from the data points directly and then averaging, as shown in the table below.

Types of error presentResult obtained from the gradient of a line of best fitResult obtained from calculating using all data points and averaging them
Perfect data – no errors1.001.00
Random error1.041.04
Random error with outlier1.041.07
Random and systematic errors1.011.47

From the table, we can see that:

  • The perfect data has a gradient of 1.
  • The random error gives a gradient is 1.04, still very close to the correct value of 1.
  • The outlier is ignored by the line of best fit, so the gradient is still 1.04, close to the correct value. Averaging over the data points would not ignore the outlier and would give a worse result of 1.07.
  • The systematic error shifts up the data by the same amount but does not change the gradient, which is still 1.01. This is still very close to the correct value of 1. However, averaging over the points, in this case, gives an incorrect answer of 1.47.

 

Common mistakes with drawing lines of best fit

The example below shows common mistakes by students when drawing lines of best fit. The exact mistakes the students have made are listed below.

Mistake 1: Missing labels

Graph 1 shown below is missing labels:

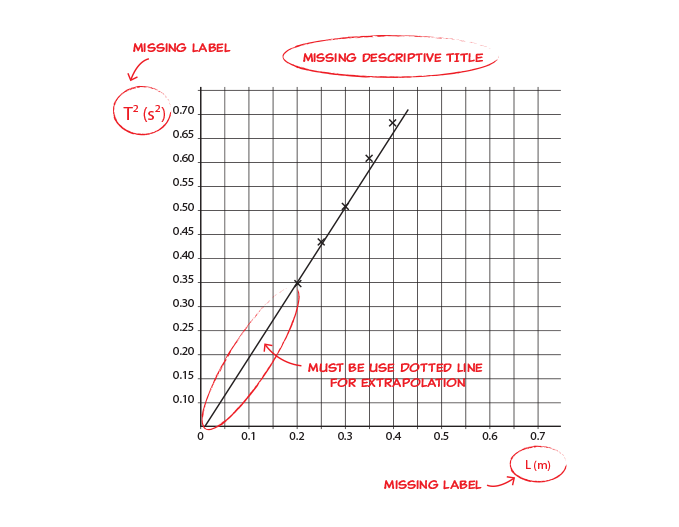
Mistakes in this graph include:

  • Missing labels for the axes
  • Missing descriptive title
  • The extrapolated line is not drawn using a dotted line

6 Common Mistakes HSC Physics Students Make in Exams

Mistake 2: Incorrect scale

Graph 2 shown below contains an incorrect scale:

 

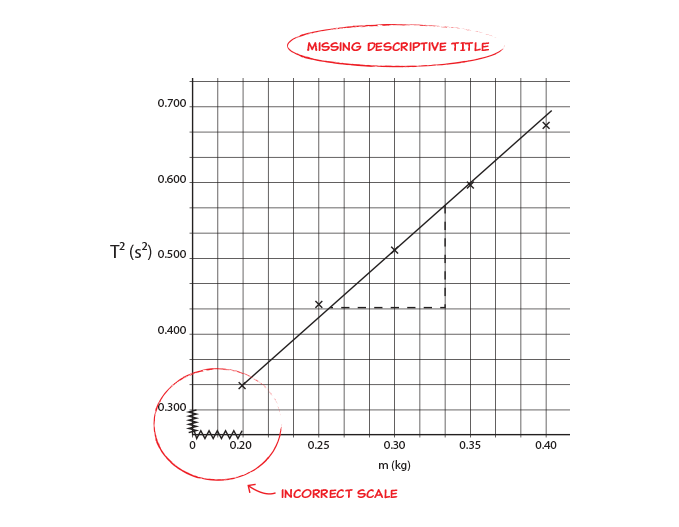
Mistakes in this graph include:

  • Incorrect scale in x and y-axes. Each division should represent the same value across each axis. For example, if each division is set a value of 0.05 at the beginning of the graph for that axis, then one division should always represent 0.05 for that axis.
  • The student should either start the scale at 0 or at 0.20 on the x-axis.

 

 

 

© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.

Related courses

More essential guides

Loading