Select a year to see courses
Select a year to see available courses
Are you struggling with Ext 1? Well, in this article, we’re going to walk you through the key parts of the Year 11 Maths Extension 1 Further Functions and Relations unit.
Further functions and relations in Extension I builds on content learnt in the Advanced stream.
In this article, we will be discussing harder absolute values, root-coefficient relationships and parametric functions. Absolute and polynomial content will be an extension of content that is taught within both previous years and the advanced course. Parametric content, however, incorporates previous knowledge of functions and relations and will be used in future topics including calculus, linear motion and projectile motion.
This free worksheet had 4 levels of difficulty to assess your knowledge.
Students should already be familiar with solving and graphing absolute values, solving and sketching parabolas, polynomials and circles.
Students can refresh their knowledge on simple equations in the following Year 10 and 11 Subject Guides:
The following section of the blog will cover the various methods of solving equations and inequalities that contain absolute values.
Graphical methods and algebraic methods to solve such equations will be provided.
This section will cover the general algebraic method which can be used to solve an equation in the form of \(|ax+b|=|cx+d|\).
Example: Find the solutions to the equation \(|5x+7|=|2x-4|\).
Step 1: Determine the critical points of the two functions inside the absolute value signs. This is done by setting the value of each function to \(0\) and solving for \(x\).
\begin{align*}
&5x+7=0; x=-\frac{7}{5}\\
&2x-4=0; x=2\\
\end{align*}
Step 2: Use these critical points to construct different intervals and find the equation which holds in each of these intervals.
For our example, we can rewrite the two absolute value functions as two piecewise functions:
\begin{align*}
&|5x+7|=
\begin{cases}
&5x+7 & \text{for} & x≥-\frac{7}{5}\\
&-(5x+7) & \text{for} & x<-\frac{7}{5}\\
\end{cases}
\end{align*}
\begin{align*}
&|2x-4|=
\begin{cases}
&2x-4 & \text{for} & x≥2 \\
&-(2x-4) & \text{for} & x<2\\
\end{cases}
\end{align*}
Case 1: \(x<-\frac{7}{5}\)
\begin{align*}
|5x+7|&=-(5x+7)\\
|2x-4|&=-(2x-4)\\
∴-(5x+7)&=-(2x-4)\\
5x+7&=2x-4\\
3x&=-11\\
x&=-\frac{11}{3}\\
\end{align*}
This solution satisfies \(x<-\frac{7}{5}\), so it is a valid solution for this branch.
Case 2: \(-\frac{7}{5}≤x<2\)
\begin{align*}
|5x+7|&=5x+7\\
|2x-4|&=-(2x-4)\\
5x+7&=-(2x-4)\\
5x+7&=-2x+4\\
7x&=-3\\
x&=-\frac{3}{7}\\
\end{align*}
This solution satisfies \(-{7}{5}≤x<2\), so it is a valid solution for this branch.
Case 3: \(x≥2\)
\begin{align*}
|5x+7|&=5x+7\\
|2x-4|&=2x-4\\
5x+7&=2x-4\\
3x&=-11
x&=-\frac{11}{3}
\end{align*}
This solution DOES NOT satisfy \(x≥2\), so it is an invalid solution for this branch
To solve this same question, we could alternatively choose to use a graphical approach. To do so, first graph the two absolute value functions on the same plot.
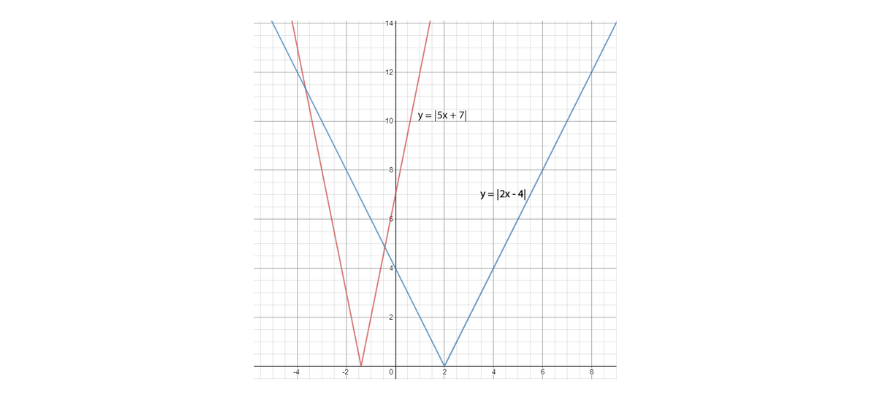
It is important to note here that the points of intersection between the two graphs correspond to the solutions of the equation we are trying to solve. A very neat sketch would give us a rough estimate for the solutions to our equation. If we want to find exact solutions, we must then proceed with an algebraic approach. We can see in the above diagram that the solutions occur when the negative branch of \(y=|5x+7|\) intersects with the negative branch of \(y=|2x-4|\) and when the positive branch of \(y=|5x+7|\) intersects with the negative branch of \(y=|2x-4|\).
This gives us two equations we can solve:
\begin{align*}
\text{1st Solution}: -(5x+7)&=-(2x-4)\\
x&=-\frac{11}{3}\\
&\text{2nd Solution}: 5x+7&=-(2x-4) \\
x&=-\frac{3}{7}\\
\end{align*}
These are the exact solutions we found with the algebraic approach we used previously!
This section will cover the general algebraic method which can be used to solve an equation in the form of \(|ax+b|=cx+d\)
Example: Find the solutions to the equation \(|3x+1|=2x+7\)
We will start by following a similar method to that of equations involving two absolute value functions. Start by rewriting the equation with the absolute value as a piecewise function.
\begin{align*}
&|3x+1|=
\begin{cases}
&3x+1 & \text{for} & 7 x≥-\frac{1}{3}\\
&-(3x+1) & \text{for} & x<-\frac{1}{3}\\
\end{cases}
\end{align*}
Now, consider each of the individual cases and find the equation which holds in each of these cases.
Case 1: \(x≥-\frac{1}{3}\)
\begin{align*}
3x+1&=2x+7\\
x&=6\\
\end{align*}
This solution satisfies \(x≥-\frac{1}{3}\), so it is a valid solution for this branch.
Case 2: \(x<-\frac{1}{3}\)
\begin{align*}
-(3x+1)&=2x+7\\
-3x-1&=2x+7\\
5x&=-8\\
x&=-\frac{8}{5}\\
\end{align*}
This solution satisfies \(x<-\frac{1}{3}\), so it is a valid solution for this branch
You can also use a graphical approach to determine the solutions of this equation. Remember that the points of intersection between the graphs correspond to solutions of the equation. A very neat sketch will give you these solutions accurately.
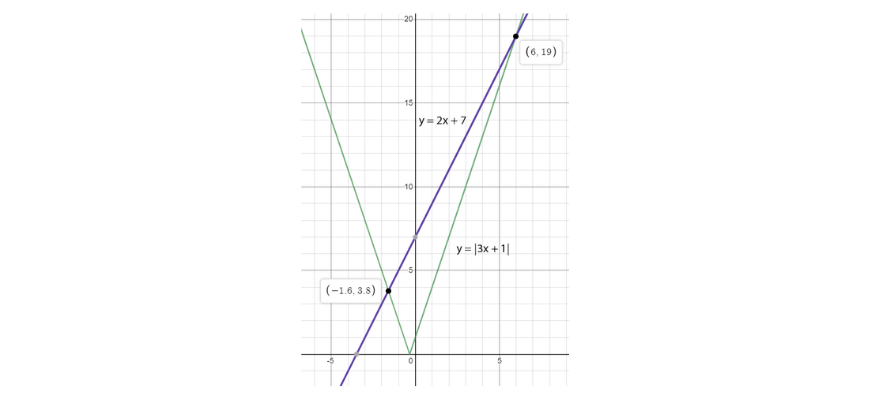
You can then proceed to determine the solutions algebraically depending on which branches the line intersects with (similar to what is done with equations involving two absolute values).
Solving absolute value inequalities is most easily done through a graphical approach. We will explore this method in the following two examples.
Example 1: \(|2x-5|<x+5\)
Step 1: Sketch the left-hand side function and the right-hand side function on the same plot.
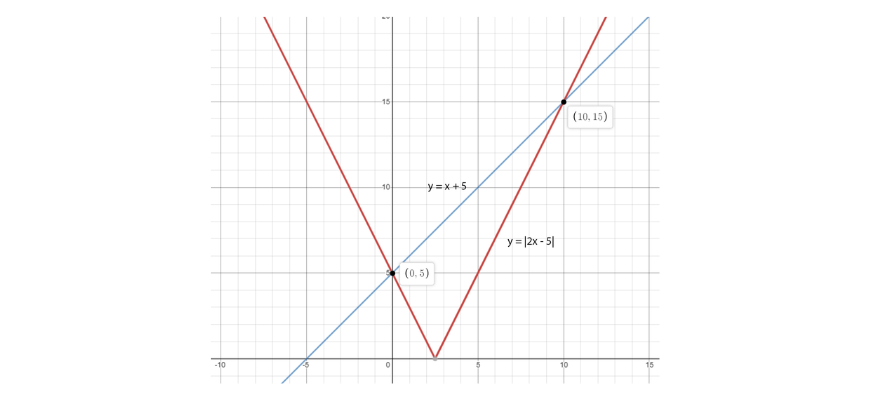
Step 2: Find the points of intersection using the methods discussed previously. Then, determine the solutions graphically.
Using the methods we discussed beforehand, we find that the points of intersection between the graphs is \(x=0\) and \(x=10\). Graphically, for \(|2x-5|<x+5\), we need to find all values of x which results in the blue curve being above the red curve. As seen in the graph, this occurs when \(0<x<10\).
Example 2: \(|x+2|≤|3x-1|\)
Step 1: Yet again, sketch the left-hand side function and the right-hand side function on the same plot.
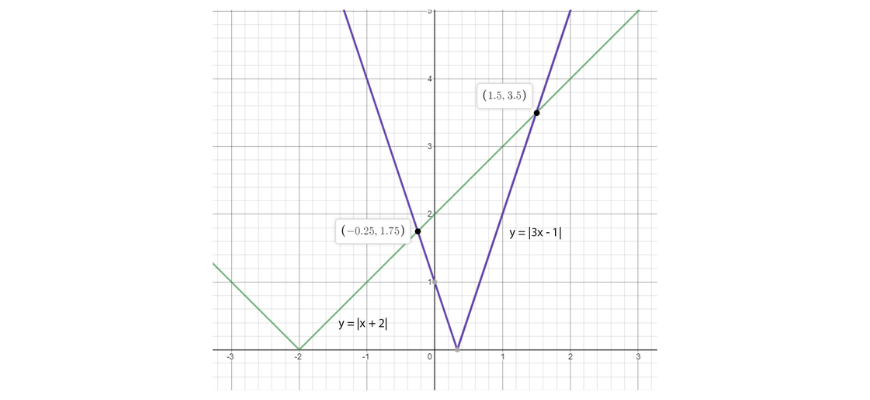
Step 2: Find the points of intersection using the methods discussed previously. Then, determine the solutions graphically.
Using the methods we discussed beforehand, we find that the points of intersection between the graphs is \(x=-0.25\) and \(x=1.5\). Graphically, for \(|x+2|≤|3x-1|\), we need to find all values of x which results in the purple curve being above the green curve. As seen in the graph, this occurs when \(x≤-0.25\) or \(x≥1.5\).
In this section, we will discuss the root-coefficient relationships for polynomials including Quadratics, Cubics and Quartics. Knowing the root-coefficient relationships allow for finding various results with the roots of a polynomial without factorizing it completely, saving many steps and time.
For a polynomial of degree two (a quadratic), then the maximum number of real roots in a quadratic equation given by \(ax^2+bx+c=0\) can have is \(2\). We can derive the root-coefficient relationships by letting the roots be \(α\) and \(β\) for \(ax^2+bx+c=0\).
Hence,
\begin{align*}
ax^2+bx+c&=a(x-α)(x-β)\\
&=a(x^2-αx-βx+αβ)\\
&=ax^2-a(α+β)x+ααβ\\
\end{align*}
If we equate the coefficients
\begin{align*}
b&=-α(α+β)-\frac{b}{a}\\
&=α+βc\\
&=ααβ\\
\frac{c}{a}&=αβ\\
\end{align*}
Therefore, the equations for the sums of roots and products of roots are:
Sums of Roots: \(α+β=-\frac{b}{a}\)
Products of Roots: \(αβ=\frac{c}{a}\)
Example 1:
The quadratic equation \(5x^2-3x+2=0\) has roots \(α\) and \(β\). Find the sums and products of roots.
The coefficients of the quadratic equation would be \(a=5\),\(b=-3\) and \(c=2\). By using the sums and products of roots formulae and substituting the coefficient values, we are able to easily find the answer.
Sums of Roots: \(α+ β= -\frac{b}{a}=-\frac{(-3)}{(5)}=\frac{3}{5}\)
Product of Roots: \(αβ=\frac{c}{a}=\frac{2}{5}\)
Cubic and Quartic root-coefficient relationships can be derived in a very similar method by assuming there are three roots and four roots respectively, expanding brackets and comparing coefficients. There are three root-coefficient relationships in cubic equations. These are:
\begin{align*}
\text{Sums of Roots:} α+β+γ&=-\frac{b}{a}\\
\text{Sum of Pairs (Two Roots):}αβ+αγ+βγ&=\frac{c}{a}\\
\text{Product of Roots:}αβγ&=-\frac{d}{a}\\
\end{align*}
For quartic equations, there are four equations. These are:
\begin{align*}
\text{Sums of Roots:} α+β+γ+δ&=-\frac{b}{a}\\
\text{Sum of Pairs (Two Roots):} αβ+αγ+αδ+βγ+βδ+γδ&=\frac{c}{a}\\
\text{Sum of Triples (Three Roots):} αβγ+αβδ+αγδ+βγδ&=-\frac{d}{a}\\
\text{Product of Roots:} αβγδ&=\frac{e}{a}\\
\end{align*}
To remember these equations easier, note that:
\begin{align*}
\text{Sum of Roots} & = -\frac{b}{a}\\
\text{Product of Roots} & = \frac{c}{a}\\
\end{align*}
Signs alternate between each subsequent equation starting with a minus in \(-\frac{b}{a}\)
The majority of questions given in exams will involve a relationship between roots, including reciprocals, multiples, equals and opposite in sign. These will always require the basic root-coefficient correlations to solve, however not all are usually required.
Some important algebraic results that will be useful include:
\begin{align*}
α^2+β^2&=(α+β)^2-2αβ\\
α^2+β^2+γ^2&=(α+β+γ)^2-2(αβ+αγ+βγ)\\
\end{align*}
For Example: Consider the equation \(4x^3+32x^2+79x+60=0\). One of the roots is equal to the sum of the other two roots. Find the value of the three roots.
Firstly, we would have to establish pronumerals for each of the roots. If we let the first and second root be α and β respectively, then the third root would be \(α+β\). The root-coefficient relationships would:
\begin{align*}
\text{Sum of Roots:}& α+β+(α+β)&=-\frac{32}{4}\\
\text{Product of Roots:}& αβ(α+β)&=-\frac{60}{4}\\
\end{align*}
Simplifying both equations
\begin{align*}
2α+2β&=-8\\
α+β&=-4
\text{and}\\
αβ(α+β)&=-15\\
\end{align*}
From here, we have already found the value of the third root \((α+β=-4)\). We can find the other two values by substitution this into the products of roots equation.
\begin{align*}
α(-4-α)(-4)&=-15\\
4α^2+16α+15&=0\\
(2α+3)(2α+5)&=0\\
∴α&=-\frac{3}{2},-\frac{5}{2}\\
\text{When} & α= -\frac{3}{2},β=-4-(-\frac{3}{2}=-\frac{5}{2}\\
\text{When}& α=-\frac{5}{2},β=-4-\frac-{5}{2}=-\frac{3}{2}\\
∴\text{Roots are}& -4,-\frac{5}{2},-\frac{3}{2}\\
\end{align*}
In this section, we will discuss parametric representation of linear, quadratic and circle relationships. A parameter is a variable that expresses two related variables (e.g. x, y) through parametric functions. Within this section, we will discuss how to eliminate variables to form the cartesian equation, standard parametric equations of lines, parabolas and circles.
An example of a parametric function would be
\begin{align*}
x&=3t\\
y&=2t-5\\
\end{align*}
From these equations, we can see that both the x and y values are linked through a parametric equation with the singular variable t. This can also be written as Parametric Coordinates as shown below
(\(3t,2t-5\))
To eliminate the parameter, simply make the parameter the subject of one equation and substitute it into the other equation.E.g. Find the Cartesian equation of a curve parametrically defined by \(x=2t\), \(y=6t-5\)
\begin{align*}
x&=2t\\
t&=\frac{x}{2}\\
\text{Substitute} \ t&=\frac{x}{2} & \text{into} \ y=6t-5\\
y&=6(\frac{x}{2})-5\\
y&=3x-5\\
\end{align*}
Converting parametric equations to cartesian equations will only result in one result. However, there are many parametric expressions for a single cartesian equation.
Straight lines can be represented parametrically in various ways. Below, we will go through the steps to turn Cartesian equations into parametric form given one parametric function.
Example:
Produce a parametric representation for the cartesian equation \(3x-2y+6=0\) given that \(x=2t-1\)
In this question, we want to find the parametric function that relates the variable \(y\) and the parameter \(t\). This can be done by simply substituting \(x=2t-1\) into \(3x-2y+6=0\) and making \(y\) the subject.
\begin{align*}
3(2t-1)-2y+6&=0\\
6t-3-2y+6&=0\\
-2y&=-6t-3\\
y&=\frac{6t+3}{2}\\
\end{align*}
To derive the parametric equation of a circle centered at the origin, we need to consider a point on the circle with radius r
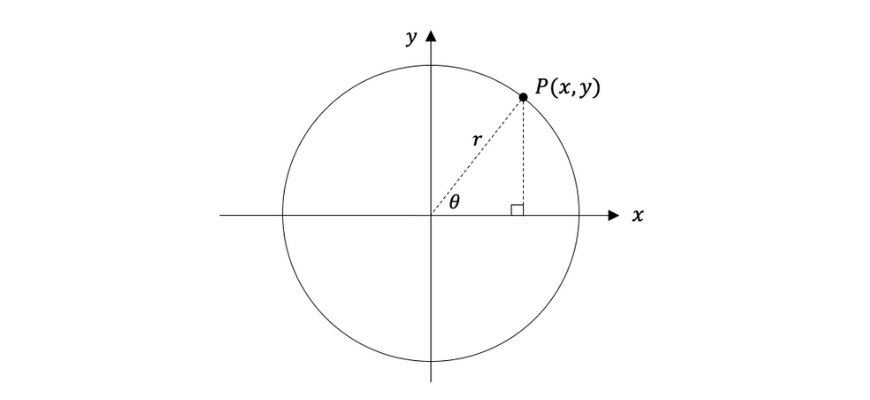
Using basic trigonometry, we can find the equations of both the \(x\) and \(y\) coordinate using the radius \(r\) and the parameter \(θ\). Therefore our standard parametric representation of a circle centered at the origin is:
\begin{align*}
x&=r\cos(θ)\\
y&=r\sin(θ)\\
\end{align*}
Where \(0≤θ≤2π\) and \(r\) is a constant value representing the radius of the circle.
For circles not centered at the origin, the parametric equations can be similarly derived. For a circle with centre (h,k) and radius r, the parametric function would be
\begin{align*}
x&=h+r\cos(θ)\\
y&=k+r\sin(θ)\\
\end{align*}
Example: Find the cartesian equation represented by the parametric equations below and describe it geometrically.
\begin{align*}
x&=-4+3 \cos(θ)\\
y&=5+3\sin(θ)\\
\end{align*}
To convert the parametric equation into the cartesian form, we would need to use the trigonometric identity \(sin^2 (θ)+cos^2(θ)=1\). For simplicity, we can make the trigonometric function the subject of both equations.
\begin{align*}
\cos(θ)&=\frac{(x+4)}{3}\\
\sin(θ)&=\frac{(y-5)}{3}\\
\end{align*}
Squaring both sides and adding the equations will result in:
\begin{align*}
\sin^2(θ)+\cos^2(θ)&=\frac{(x+4)^2}{3}+\frac{(y-5)^2}{3}\\
1&=\frac{(x+4)^2+(y-5)^2}{3}\\
3&=(x+4)^2+(y-5)^2\\
\end{align*}
The parametric form of the parabola is dependent on the form \(x^2=4ay\), where \(a\) is the focal length. The standard parametric equations of the parabola are
\begin{align*}
x&=2ap\\
y&=ap^2\\
\end{align*}
Example: Find the standard parametric equations of \(y=-\frac{1}{8} x^2\).
To begin, we need to rearrange the equation into the form \(x^2=4ay\).
\begin{align*}
&x^2=-8y\\
\end{align*}
By comparing with the standard form, we can see that the focal length \(a\) is \(2\). However, despite focal length being \(2\), it is of negative concavity. We can simply substitute \(a=2\) into the standard parametric equations.
\begin{align*}
x&=-4p\\
y&=-2p^2\\
\end{align*}
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.
