Part 4: Projectile Motion | Beginner’s Guide to Year 12 Ext 1 Maths

In this article, we give you the run-down on projectile motion so you can launch your Maths marks!
Beginner's Guide to Year 12 Ext 1 Maths projectile motion diagram

Do you need to get your Extension 1 Maths marks on the right trajectory? This guide on Projectile Motion for Extension 1 will help you change the path of your marks!

In this article, we’ll discuss

 

Get more practice with a range of Projectile Motion questions!

Free Y12 Maths Ext1 Projectile Motion Worksheet

A worksheet to test your knowledge.

Download now

Year 12 Mathematics Extension 1: Projectile Motion

The motion or mechanics of projectiles has been a human concern since the first man threw a rock. The first accurate description of projectile motion was made by Galileo, who broke down motion into separate horizontal and vertical components. This revolutionary insight is what we will be investigating in this blog.

 

NESA Syllabus Outcomes

Students should:

  • understand the concept of projectile motion, and model and analyse a projectile’s path assuming that:
    • the projectile is a point
    • the force due to air resistance is negligible
    • the only force acting on the projectile is the constant force due to gravity, assuming that the projectile is moving close to the Earth’s surface
  • model the motion of a projectile as a particle moving with constant acceleration due to gravity and derive the equations of motion of a projectile represent the motion of a projectile using vectors
    • recognise that the horizontal and vertical components of the motion of a projectile can be represented by horizontal and vertical vectors
    • derive the horizontal and vertical equations of motion of a projectile
    • understand and explain the limitations of this projectile model
  • use equations for horizontal and vertical components of velocity and displacement to solve problems on projectiles
  • apply calculus to the equations of motion to solve problems involving projectiles

 

Assumed Knowledge

Students are assumed to have a basic understanding of quadratics, trigonometry, calculus and vectors. This includes the topics of differentiation, integration, rates of change and motion in a line. Students should also be familiar with vector notation and the vector concepts of direction and magnitude.

 

Definition of Projectile Motion

A projectile is any object that moves through the air and is subject to only a single force, gravity. This means that self-propelled objects such as rockets or buoyant objects like balloons are not considered to be projectiles. For Extension 1, projectiles are represented as points and the effects of air resistance are also assumed to be negligible. Under these simplifications, a projectile’s trajectory can be plotted on a Cartesian plane as a parabola.

 

Projectile Motion Decomposition

We may decompose projectile motion into both horizontal and vertical components that are parametric in terms of \(t\).

Horizontal displacement (\(x\))Vertical displacement (\(y\))
Horizontal velocity (\(\dot{x}\))Vertical velocity (\(\dot{y}\))
Horizontal acceleration (\(\ddot{x}\))Vertical acceleration (\(\ddot{y}\))

Example 1:

Hugh throws a stone into the air with an initial speed of \(8ms^{-1}\) at an angle of elevation of \(60°\). Determine the horizontal and vertical components of the stone’s initial velocity.

 

Solution:

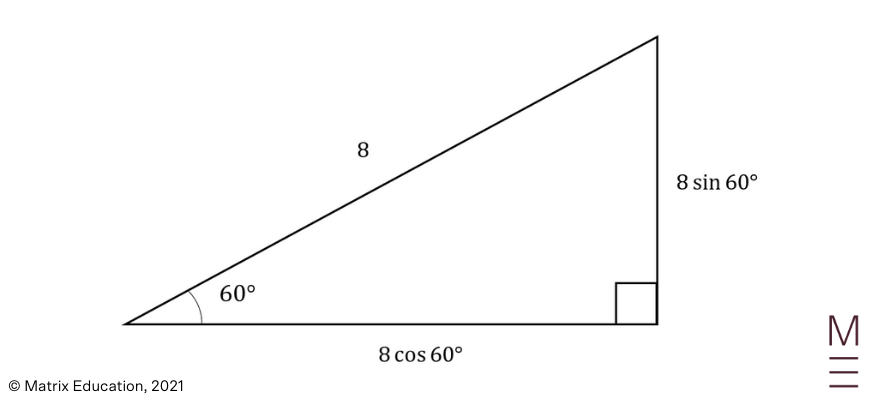
Horizontal component of velocity \((\dot{x})\):

\begin{align*}
\dot{x} &=8 cos⁡(60°)\\
&=8×\frac{1}{2}\\
&=4 ms^{-1}\\
\end{align*}

Vertical component of velocity \(\dot{y}\):

\begin{align*}
\dot{y} &=8 sin⁡(60°)\\
&=8×\frac{\sqrt{3}}{2}\\
&=4\sqrt{3} ms^{-1}
\end{align*}

 

Vertical Component

From the definition of projectile motion, we assume that the only force acting on a projectile is the downwards force of gravity. We encapsulate this as

\(\ddot{y}=-g\)

where \(g\) represents the acceleration due to gravity. On Earth this is roughly \(g=9.81 ms^{-2}\) but more often approximated as \( g=10 ms^{-2}\).

Recall that the acceleration, velocity and displacement of an object have the following relationships.

\begin{align*}
\dot{y}&=\frac{dy}{dt}\\
\ddot{y}&=\frac{d\dot{y}}{dt}= \frac{d^2y}{dt^2}\\
\end{align*}

 

Example 1:

George fires a gun directly upwards. Assume that there is no wind so that the bullet has no horizontal displacement. The bullet escapes the chamber at a speed of \(600ms^{-1}\). If George fires the gun at a height of \(2.2m\) from the ground, find the equation for the height of the bullet as a function of time \(t\). You may assume that the acceleration due to gravity is \(10ms^{-2}\).

 

Solution:

\begin{align*}
\ddot{y}&=-10\\
\text{Integrating }\ddot{y}\\
\dot{y} &=-10t+C_1\\
\text{Substituting } t&=0, \ \dot{y}=600\\
600&=-10×0+C_1\\
C_1&=600\\
∴\dot{y}&=-10t+600\\
\text{Integrating } \dot{y}& \text{ gives}\\
y&=-5t^2+600t+C_2\\
\text{Substituting } t&=0, \ y=2.2\\
2.2 &=-5×0^2+600×0+C_2\\
C_2 &=2.2\\
∴y&= -5t^2+600t+2.2\\
\end{align*}

 

 

Horizontal Component

Now we focus on the horizontal component. Since the only the force on a projectile is gravity, then there are no forces acting horizontally. That is, our horizontal acceleration is

\(\ddot{x}=0\)

Again, the acceleration, velocity and displacement of an object has the following relationships.

\begin{align*}
\dot{x}&=\frac{dx}{dt}\\
\ddot{x}&=\frac{d\dot{x}}{dt}=\frac{d^2 x}{dt^2}\\
\end{align*}

A projectile is always assumed to be initially positioned at the origin, unless suggested otherwise by the question.

 

Example 1:

A trebuchet is stationed \(300m\) away from a castle wall. When fired, it launches a stone with a speed of \(56m/s\) at an angle of elevation of \(55°\). Given that the stone collides with the castle wall, determine how long it takes for the castle wall to be destroyed from the moment that a trebuchet is fired.

 

Solution:

Decomposing the initial velocity:

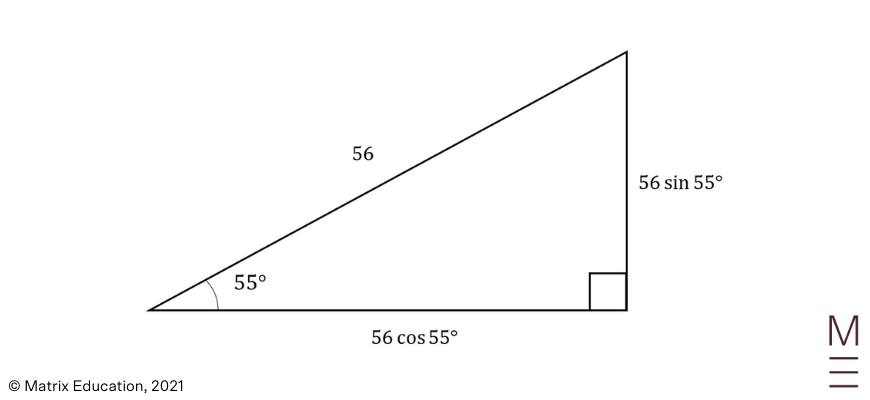
\begin{align*}
\ddot{x}&=0\\
\text{Integrating } \ddot{x}& \text{ gives}\\
\dot{x} &=C_1\\
\text{Substituting } t&=0, \dot{x}=56 cos⁡(55°)\\
C_1&=56 cos⁡(55°)\\
∴\dot{x}&=56 cos⁡(55°)\\
\text{Integrating } \dot{x}& \text{ gives}\\
x &=56 cos(55°) t+C_2\\
\text{Substituting } t&=0, x=0:\\
0 &=56 cos⁡(55°)×0+C_2\\
C_2&=0\\
∴x&=56 cos⁡(55°) t\\
\text{Since the wall is 300 m away, substitute } x&=300\\
300&=56 cos⁡(55°)t\\
t&= \frac{300}{56 cos⁡(55°)}\\
&≈9.34 s \ \ \text{(2 d.p.)}\\
\end{align*}

 

Projectile Motion with Vectors

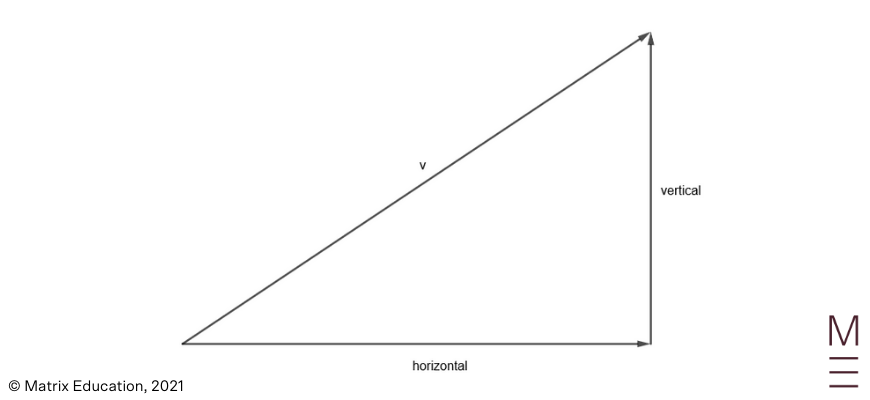
The motion of a projectile can be represented by vectors in two dimensions. Vectors can be used to quantify the acceleration, velocity and displacement of a projectile flying through the air.
The definitions of the unit vectors \(i= \binom{1}{0}\), \(j= \binom{0}{1}\) will be useful for the following equations.

\(r=xi+yj\)

where
\begin{align*}
r &= \text{displacement vector}\\
x &= \text{horizontal displacement}\\
y &= \text{vertical displacement}\\
\end{align*}

\(v=\dot{x}i+\dot{y}j\)

where
\begin{align*}
v &= \text{velocity vector}\\
\dot{x}&= \text{horizontal velocity}\\
\dot{y}&= \text{vertical velocity}\\
\end{align*}

Note that the magnitude of the velocity vector is the same as the speed of the projectile.

\(|v|=speed\)

Also, the direction of the velocity is equal to the direction that the projectile is travelling.

\(tan⁡θ=\frac{\dot{y}}{\dot{x}}\)

\(a=\ddot{x}i+\ddot{y}j\)

where
\begin{align*}
a &= \text{acceleration vector}\\
\ddot{x}&= \text{horizontal acceleration}\\
\ddot{y} &= \text{vertical acceleration}\\
\end{align*}

In Extension 1, the projectile motion acceleration vector is always

\(a=-gj\)

where \(g\) may be approximated to a value or remain a pronumeral.

Projection motion questions will usually ask for some property such as the projectile’s maximum height, time of flight or horizontal range. It is up to you to interpret and calculate these quantities from our horizontal and vertical decompositions.

 

Example 1:

Ella was playing fetch with her dog at the park. She threw a tennis ball with a speed of \(15ms^{-1}\) and an initial angle of \(45°\) from the horizontal. Assume that \(g=10 ms^{-2}\).

(a) Find the velocity vector for the tennis ball.

(b) Find the position vector for the tennis ball.

(c) Determine the maximum height reached by the tennis ball.

(d) How far did the ball land from Ella’s position?

 

Solution:

(a)

Decomposing initial velocity:

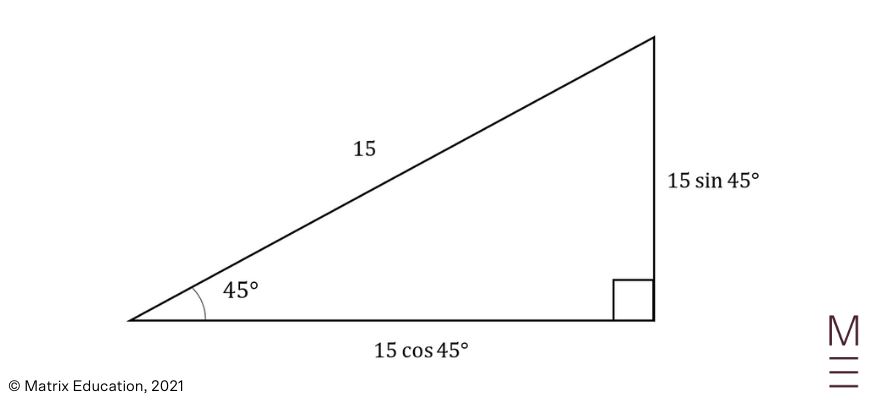
\begin{align*}
a&=-10j\\
\text{Integrating }&\text{a gives}\\
v&=C_1 i+(-10t+C_2 )j\\
\text{Substituting }t&=0 \text{ and }v=15 cos⁡(45°) i+15 sin⁡(45°) j\\
15 cos⁡(45°)i+15 sin⁡(45°)j&=C_1 i+(-10×0+C_2 )j\\
C_1&=15 cos⁡(45°)\\
&=\frac{15}{\sqrt{2}}\\
C_2&=15 sin⁡(45°)\\
&=\frac{15}{\sqrt{2}}\\
∴v&=\frac{15}{\sqrt{2}} i+\left(-10t+\frac{15}{\sqrt{2}}\right)j\\
\end{align*}

(b)

\begin{align*}
\text{Integrating }v& \text{ gives}\\
r&=\left(\frac{15}{\sqrt{2}} t+C_3 \right)i+\left(-5t^2+\frac{15}{\sqrt{2}} t+C_4 \right)j\\
\text{Substituting }t&=0, r=0i+0j\\
0i+0j&=\left(\frac{15}{\sqrt{2}}×0+C_3 \right)i+\left(-5×0^2+\frac{15}{\sqrt{2}}×0+C_4 \right)j\\
C_3&=0\\
C_4&=0\\
∴r&=\left(\frac{15}{\sqrt{2}} t\right)i+\left(-5t^2+\frac{15}{\sqrt{2}} t\right)j\\
\end{align*}

(c)

\begin{align*}
\text{The maximum height is reached when }\dot{y}&=0\\
-10t+\frac{15}{\sqrt{2}}&=0\\
t &=\frac{3}{2\sqrt{2}}\\
\text{Substituting }t&=\frac{3}{2\sqrt{2}}\text{ into }y=-5t^2+\frac{15}{\sqrt{2}} t\\
y&=-5(\frac{3}{2\sqrt{2}})^2+\frac{15}{\sqrt{2}} (\frac{3}{2\sqrt{2}})
&= \frac{45}{8}\\
∴ \text{The maximum height reached by } & \text{the ball is }\frac{45}{8} m.\\
\end{align*}

(d)

\begin{align*}
\text{The ball lands when }y&=0\\
-5t^2+\frac{15}{\sqrt{2}} t&=0\\
-5t(t-\frac{3}{\sqrt{2}})&=0\\
t&=0,\frac{3}{\sqrt{2}}\\
t&=0 \text{ is when the ball is initially in Ella’s hands, }\\
\text{so we will use }t&=\frac{3}{\sqrt{2}}\\
\text{Substituting }t=\frac{3}{\sqrt{2}} \text{ into } x=\frac{15}{\sqrt{2}} t\\
x&=\frac{15}{\sqrt{2}}×\frac{3}{\sqrt{2}}\\
&=\frac{45}{2}\\
∴ \text{Ball landed 22.5 m}&\text{ from Ella}\\
\end{align*}

 

Concept Check Questions

1. David threw a ball horizontally from the top of a balcony \(20m\) high. The ball was projected with a speed of \(16m/s\). You may assume that \(g=10ms^{-2}\).

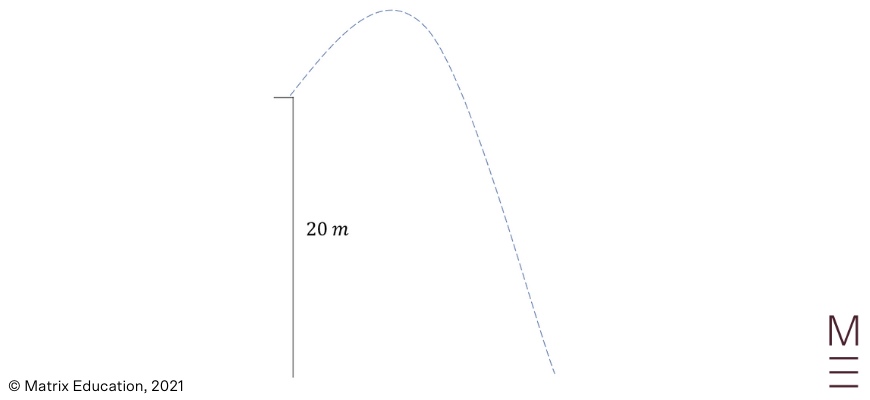
(a) Find the velocity vector of the ball.

(b) Find the displacement vector of the ball.

(c) How long did the ball take to strike the ground?

(d) How far from the base of the balcony did the ball strike the ground?

 

2. Marcus was practising his javelin-throwing in the forest. He threw a javelin with a speed of \(30ms^{-1}\) at an angle of elevation of \(62°\). You may assume that \( g=10 ms^{-2}\).

(a) Find the velocity vector of the javelin.

(b) Find the displacement vector of the javelin.

(c) Determine the maximum height that the javelin achieves.

(d) Find the Cartesian equation for the trajectory of the javelin.

(e) If there was a \(30 m \) tall oak tree that was \( 55 m\) from Marcus, would the thrown javelin pass over the tree?

 

Concept Check Solutions

1.

(a)

\begin{align*}
a&=-10j\\
\text{Integrating a }&\text{gives}\\
v&=C_1 i+(-10t+C_2 )j\\
\text{Substituting } t&=0 \text{ and }v=16i\\
16i&=C_1 i+(-10×0+C_2 )j\\
C_1&=16\\
C_2&=0\\
∴v&=16i+(-10t)j\\
\end{align*}

(b)

\begin{align*}
\text{Integrating v }&\text{gives}\\
r&=(16t+C_3 )i+(-5t^2+C_4 )j\\
\text{Substituting }t&=0, r=20j\\
20j&=(16×0+C_3 )i+(-5×0^2+C_4 )j\\
C_3&=0\\
C_4&=20\\
∴r&=(16t)i+(-5t^2+20)j\\
\end{align*}

(c)

\begin{align*}
\text{The ball lands when y}&\text{=0}\\
-5t^2+20&=0\\
-5(t^2-4)&=0\\
-5(t-2)(t+2)&=0\\
t&=-2,2\\
∴ \text{The ball strikes the ground 2 sec}&\text{onds after being thrown}\\
\text{(negative time value implies the ball}&\text{ hits the ground before it is thrown)}\\
\end{align*}

(d)

\begin{align*}
\text{Substituting }t&=2 \text{ into }x=16t\\
x&=16×2\\
&=32\\
∴ \text{The ball strikes the ground } &\text{32 m from the base of the balcony}\\
\end{align*}

2.

(a)

Decomposing initial velocity:

 

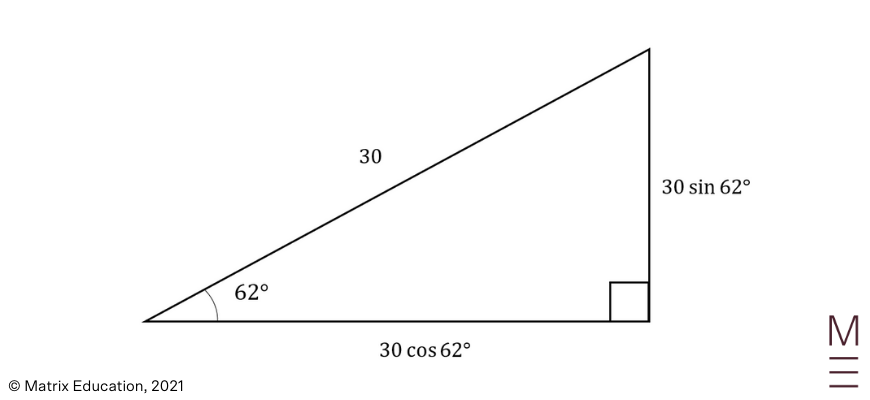
\begin{align*}
a&=-10j\\
\text{Integrating a }& \text{gives}\\
v&=C_1 i+(-10t+C_2 )j\\
\text{Substituting }t&=0 \text{ and }v=30 cos⁡(62°) i+30 sin⁡(62°) j\\
30 cos⁡(62°) i+30 sin⁡(62°) j&=C_1 i+(-10×0+C_2 )j\\
C_1&=30 cos⁡(62°)\\
C_2&=30 sin⁡(62°)\\
∴v&=30 cos⁡(62°)i+(-10t+30 sin⁡(62°) )j\\
&≈14.08i+(-10t+26.49)j\\
\end{align*}

(b)

\begin{align*}
\text{Integrating v }&\text{gives}\\
r&=(30 cos⁡(62°)t+C_3 )i+(-5t^2+30 sin⁡(62°)t+C_4 )j\\
\text{Substituting }t&=0, r=0\\
0&=(30 cos⁡(62°)×0+C_3 )i+(-5×0^2+30 sin⁡(62°)×0+C_4 )j\\
C_3&=0\\
C_4&=0\\
∴r&=(30 cos⁡(62°)t)i+(-5t^2+30 sin⁡(62°)t)j\\
\end{align*}

(c)

\begin{align*}
\text{The maximum height is}& \text{ reached when }\dot{y}=0\\
-10t+30 sin⁡(62°)&=0\\
t&=3 sin⁡(62°)\\
&≈2.65\\
\text{Substituting }t&=3 sin⁡(62°)\text{ into }y=-5t^2+30 sin⁡(62°)t\\
y&=-5(3 sin⁡(62°) )^2+30 sin⁡(62°)×3 sin⁡(62°)\\
&=45 sin^2⁡(62°)\\
&≈35.08\\
\text{The maximum height}& \text{ reached by the javelin is 35.08 m} (2 d.p.)\\
\end{align*}

(d)

\begin{align*}
x&=30 cos⁡(62°)t\\
t&= \frac{x}{30 cos⁡(62°) }\\
\text{Substituting } t&=\frac{x}{30 cos⁡(62°) } into y=-5t^2+30 sin⁡(62°)t\\
y&=-5\left(\frac{x}{30 cos⁡(62°) }\right)^2+30 sin⁡(62°)×\frac{x}{30 cos⁡(62°)}\\
&=-\frac{x^2}{180 cos^2⁡(62°)}+x tan⁡(62°)\\
\end{align*}

(e)

\begin{align*}
\text{Substituting }x&=55\text{ into the Cartesian equation}\\
y&=-\frac{55^2}{180 cos^2⁡(62°) }+55 tan⁡(62°)\\
&≈27.19\\
\text{Since 27.19 }&\text{< 30, then the javelin would collide with the 30 m tall tree}\\
\end{align*}

 

Projectile your skills to Math success

At Matrix, our HSC experts guide you through all Maths Ext 1 concepts. You also receive comprehensive resources with countless of practice questions to help refine your skills. Learn more now!

Ace Maths Ext 1 with Matrix+

Expert teachers, weekly quizzes, one-to-one help! Learn at your own pace, wherever you are.

 View a sample lesson

© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.

Related courses

More essential guides

Loading