Welcome to Matrix Education
To ensure we are showing you the most relevant content, please select your location below.
Select a year to see courses
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Learn online or on-campus during the term or school holidays
Get HSC exam ready in just a week
Select a year to see available courses
Science guides to help you get ahead
Science guides to help you get ahead

Feeling a bit directionless when studying vectors? In this article, we give you a comprehensive introduction to vectors for Year 12 Maths Ext 1 so you can find your way to a Band 6.
A worksheet to test your knowledge. Fill out your details below to get this resource emailed to you. "*" indicates required fields
Free Y12 Maths Ext1 Introduction to Vectors Download

Free Y12 Maths Ext1 Introduction to Vectors Download
Understanding how vectors operate plays a crucial role in visualising basic operations such as addition, subtraction and multiplication on a two-dimensional plane, which will then enable students to solve and prove harder geometric properties and applications.
The NESA syllabus outcomes for Year 12 Maths Extension 1 students are:
Students should already be familiar with basic algebraic operations, geometry, trigonometry and coordinate geometry.
A vector is a quantity which has both magnitude and direction. For example, a force of 60 Newtons is applied to the ground. This means that the force’s magnitude is 60 and its direction is downwards, towards the ground.
A vector can be denoted using boldface, \(\bf{u}\), an arrow above the variable, \(\vec{u}\), or a tilde under the variable, \(\stackrel{\rm u}{\rm \text{~}}\). A vector running from point \(A\) to point \(B\) is denoted by \(\vec{(AB)}\).
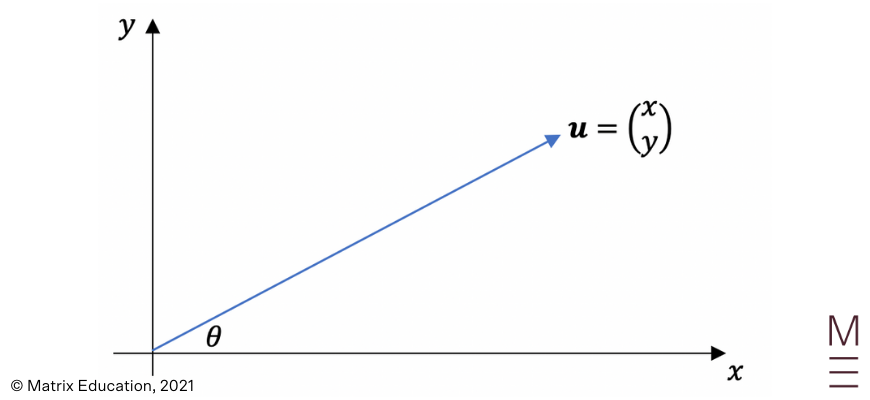
The diagram above represents vector u, which is simply an arrow: The diagram above represents vector \(\bf{u}\), which is simply an arrow: The magnitude of \(\bf{u}\), denoted \(|\bf{u}|\), is the length of the arrow. The direction of \({\bf u}\), denoted \(θ\), is the direction that the arrow is pointing towards. The pointy end of the arrow is called the head, and the other end is called the tail.
Vectors can also be represented algebraically by placing them in the (\(x,y\)) plane:
\({\bf u} \ = \left(\ _y^x \right) \ = (x,y)\)
Example 1:
Which of the following is the correct notation of a vector?
\(\vec{(AB)}, \ {\bf u}, \ V_4, \ OP, \ \stackrel{\rm m}{\rm \text{~}}\)
Solution 1:
\(\vec{(AB)}, \ , {\bf u}, \ \stackrel{\rm m}{\rm \text{~}}\)
Example 2:
Express each vector in the diagram below in column vector and Cartesian forms:
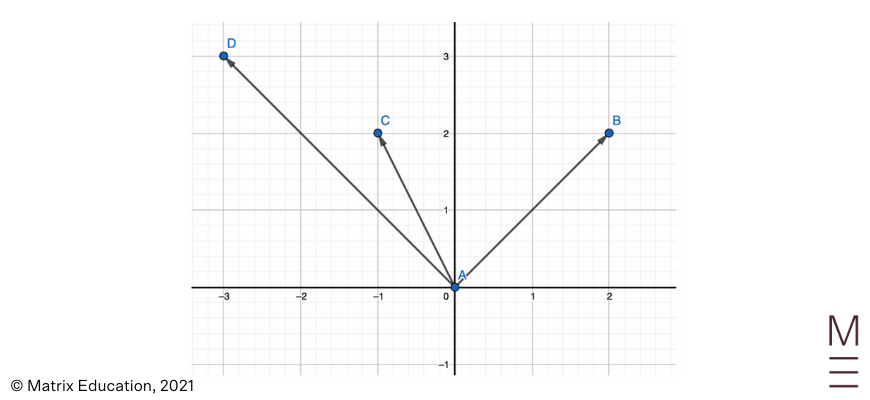
| Vector | Column vector form | Cartesian form |
| \(\vec{AB} \) | \(\left({2}\atop{2}\right) \) | \( (2,2)\) |
| \(\vec{AC} \) | \(\left( {-1} \atop {2} \right) \) | \((-1,2) \) |
| \(\vec{AD} \) | \( \left( {-3} \atop {2} \right)\) | \( (-3,3)\) |

The diagram above contains unit vectors, a position vector, a displacement vector, as well as the standard two-dimensional perpendicular unit vectors:
Using the standard two-dimensional perpendicular unit vectors, we can represent vectors in a third way, the component form. Knowing that \({\bf i} = \left( {1}\atop{0}\right)\) and \({\bf j} = \left( {1}\atop{0}\right)\), the vector \({\bf u}\) can be expressed as:
\({\bf u} = \left( {x}\atop{y}\right)=(x,y)=x{\bf i}+y{\bf j}\)
The coefficient of \({\bf i}\) is called the x-component, and the coefficient of \({\bf j}\) is called the y-component.
Example 1:

Solution 1:
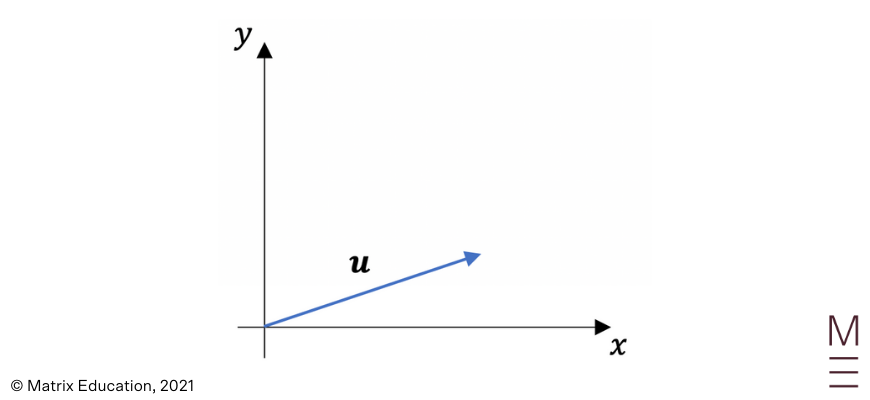
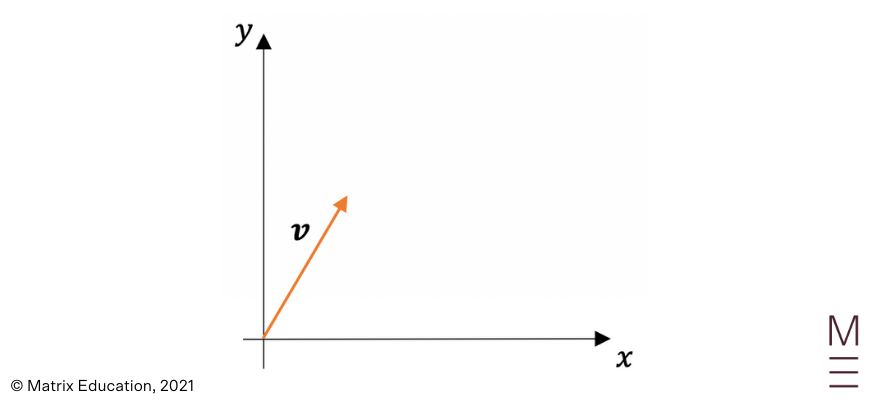
When adding vectors together, we must consider both their magnitude and direction. Vectors are added using the head to tail method:
and

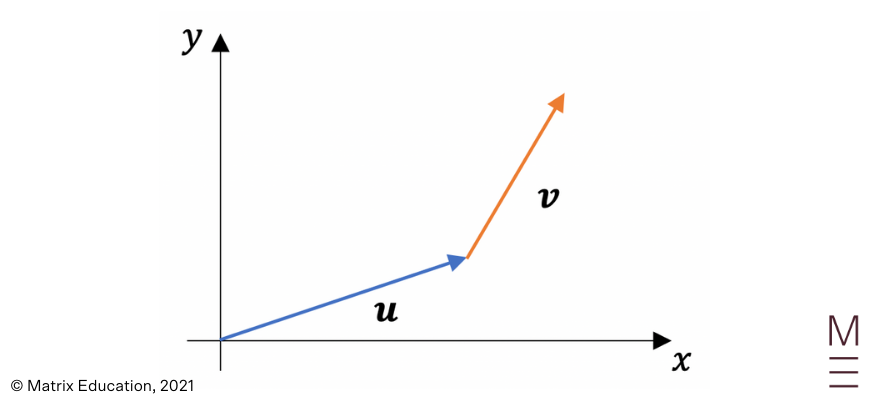
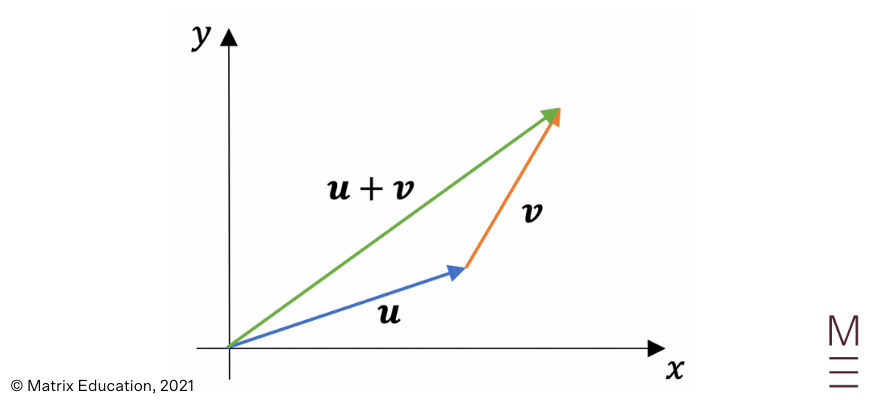
Subtracting vectors is the equivalent of adding the negative vector. The negative vector is a vector which has the same magnitude but opposite direction. We can once again use the head to tail method for the subtraction of vectors:

and
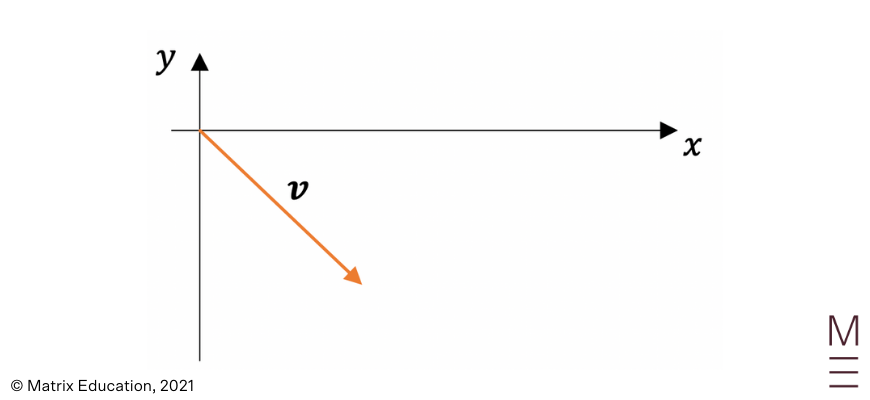
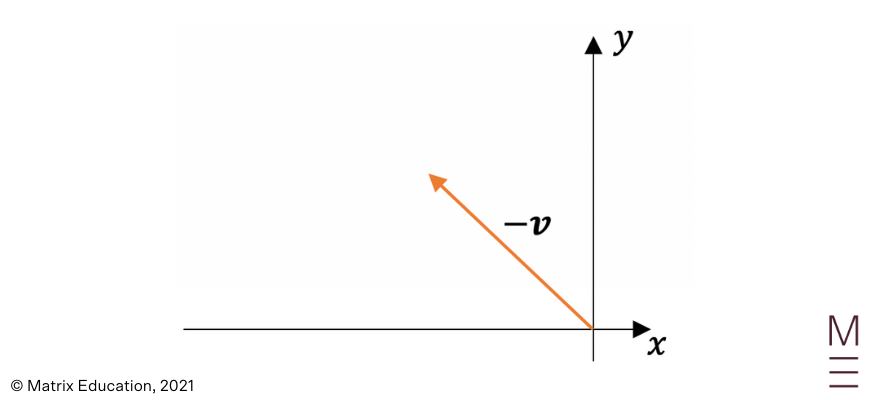
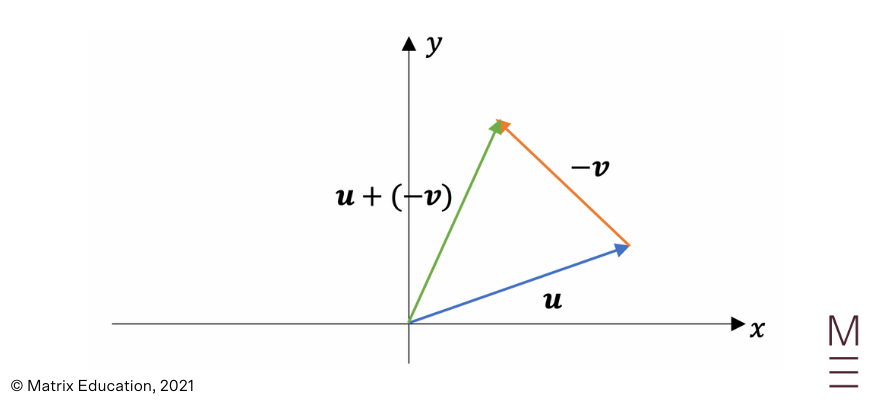
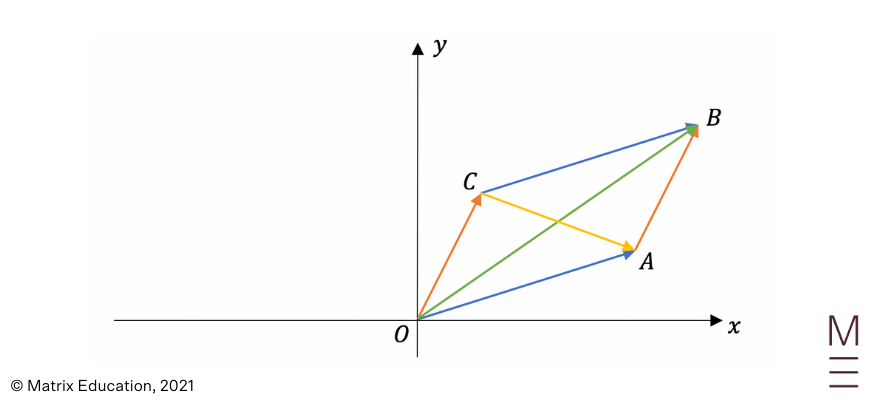
From the diagram above, we can see that vectors \(\vec{OA}\) and \(\vec{CB}\) are equal to each other, and vectors \(\vec{OC}\)and \(\vec{AB}\)are equal to each other. These four vectors form a parallelogram.
\(\vec{OB}=\vec{OA} + \vec{AB}\), and \(\vec{CA}=\vec{OA} -\vec{OC}\), which are the diagonals of the parallelogram.
Example 1:
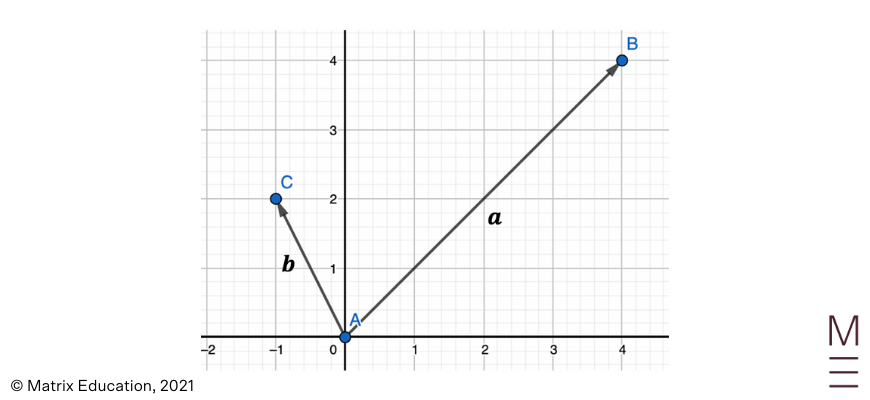
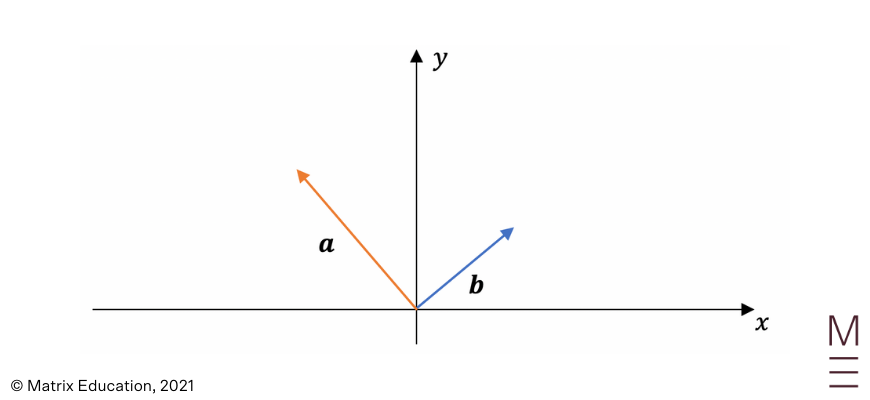
Given vectors \({\bf a}\) and \({\bf b}\) as below:
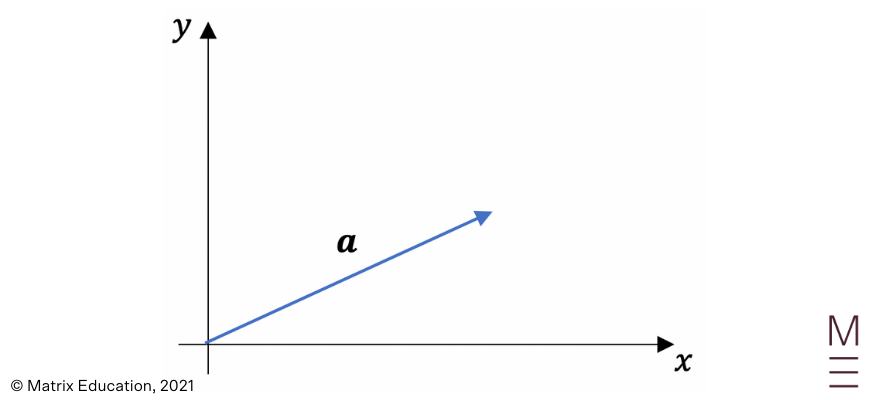
and

Use the given information to draw the following vectors:
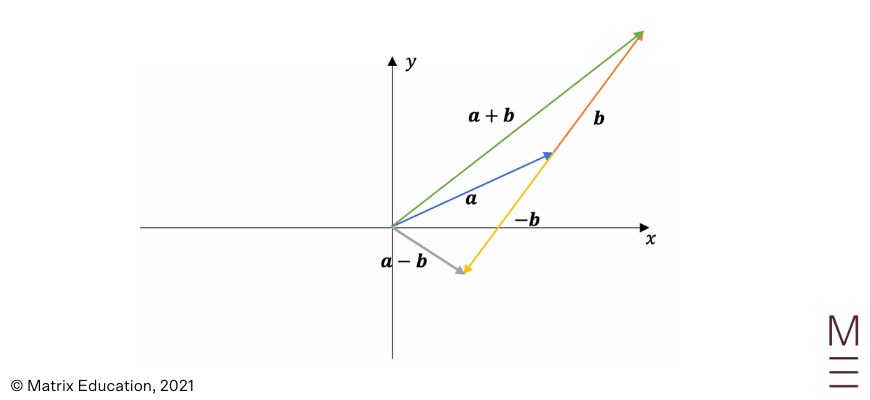
a) \({\bf a}+{\bf b}\)
b) \({\bf a}-{\bf b}\)
Example 1:
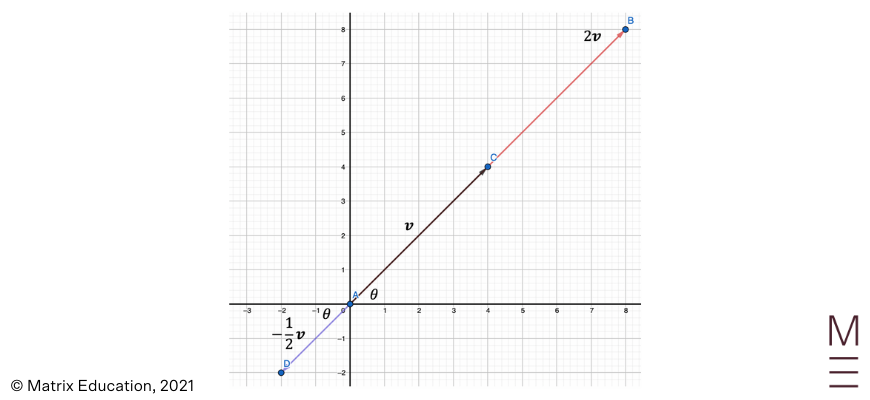
Given vectors \({\bf v}\) and \({\bf v}\) as per below:
Use the given information to draw the following vectors:
a)\(\frac{1}{2} {\bf a}\)
b)\(-3{\bf b}\)
c) \(\frac{1}{2} {\bf a} -3{\bf b}\)
Solution 1:
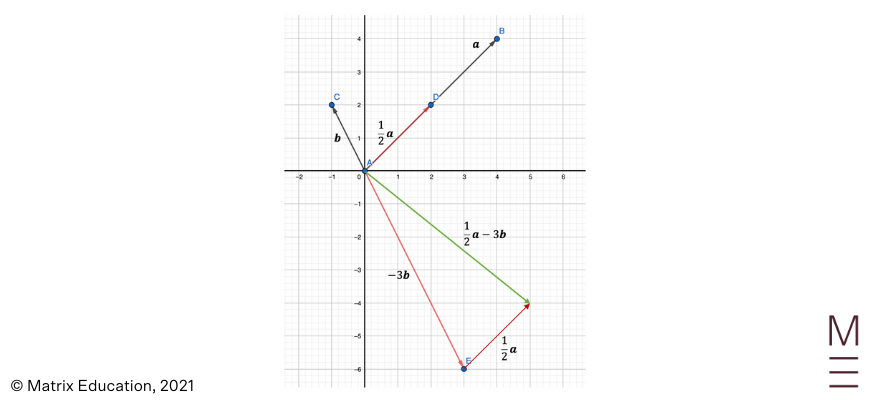
1. Given vectors \({\bf a}\) and \({\bf b}\) as per below:
Use the given information to draw the following vectors:
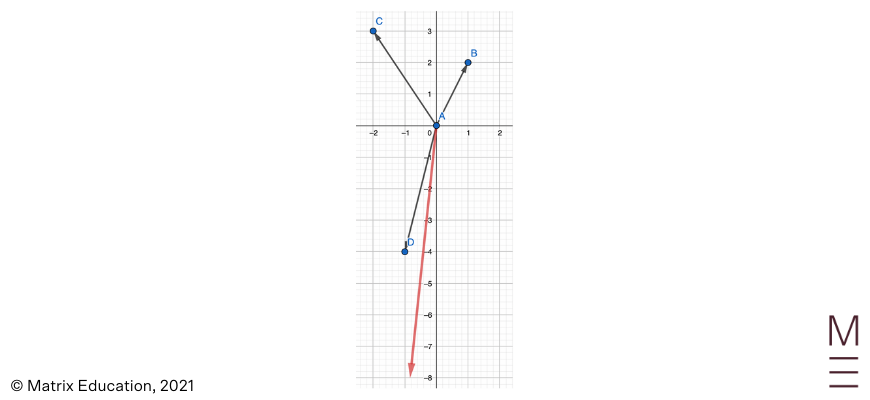
2. Let \(\vec{AB} \ \left( {1}\atop{2}, \right) \vec{AC} = \left( {-2} \atop {3} \right) \) and \( \vec{AD} \ = \left( {-1} \atop {-4} \right)\). Draw the following vectors and identify their positions:
1.
1. \({\bf -b}\)
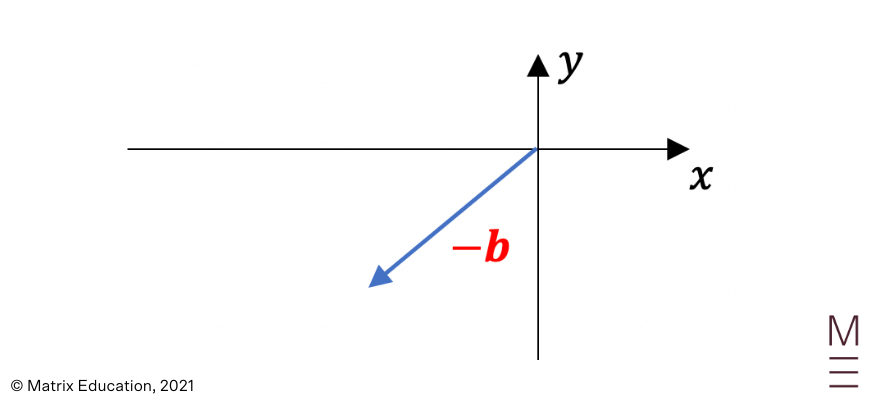
2. \({\bf a} + {\bf b}\)
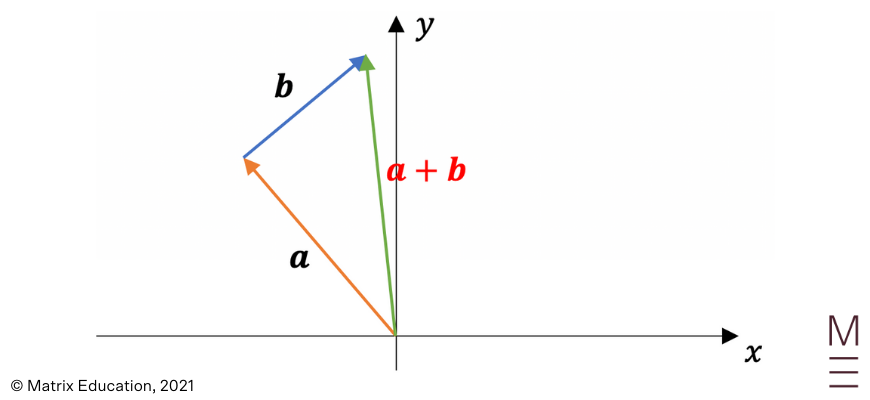
3. \({\bf a} – {\bf b}\)
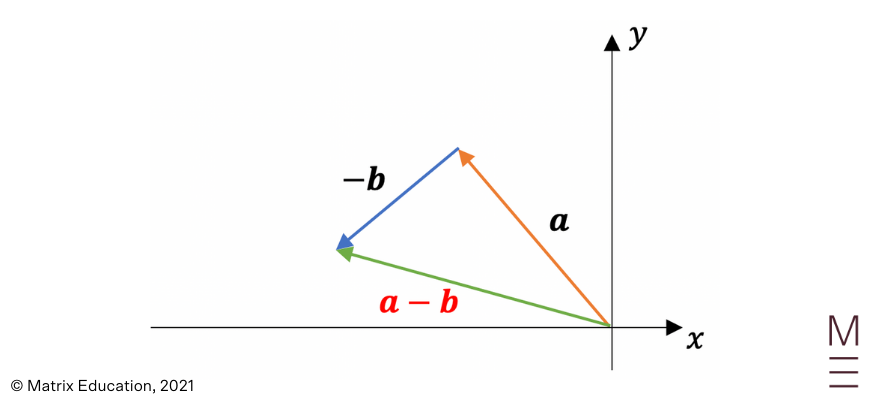
4. \({\bf b} – {\bf a}\)
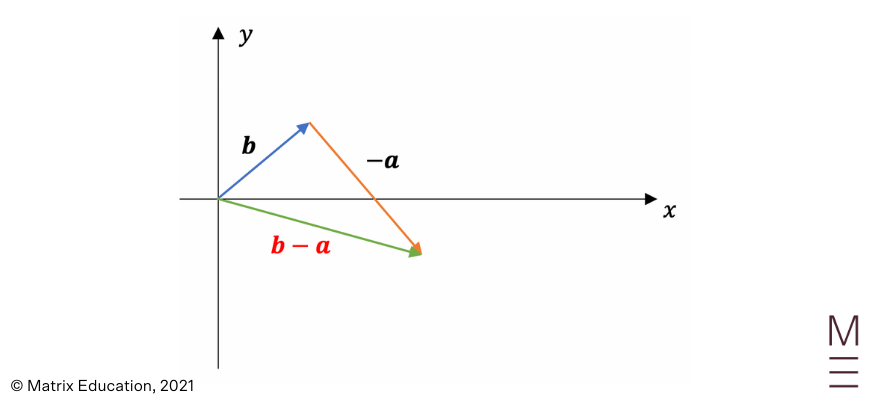
2.
In the solutions below, the vectors in red represent the answer
1. \( 2 \vec{AB}\)
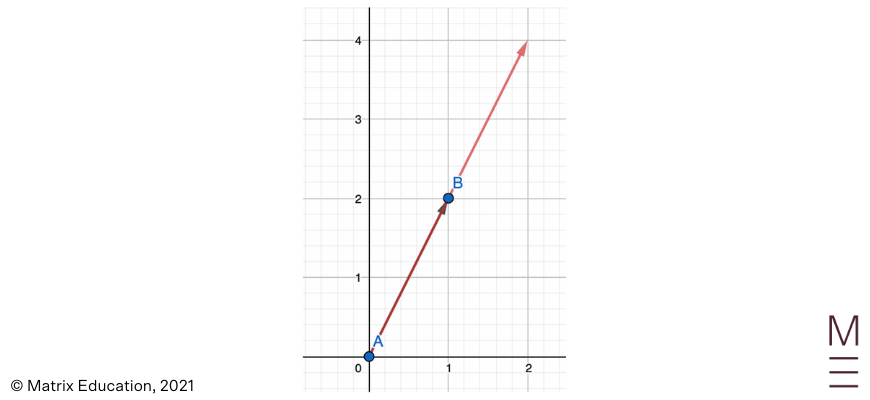
2. \(-3 \vec{AC}\)
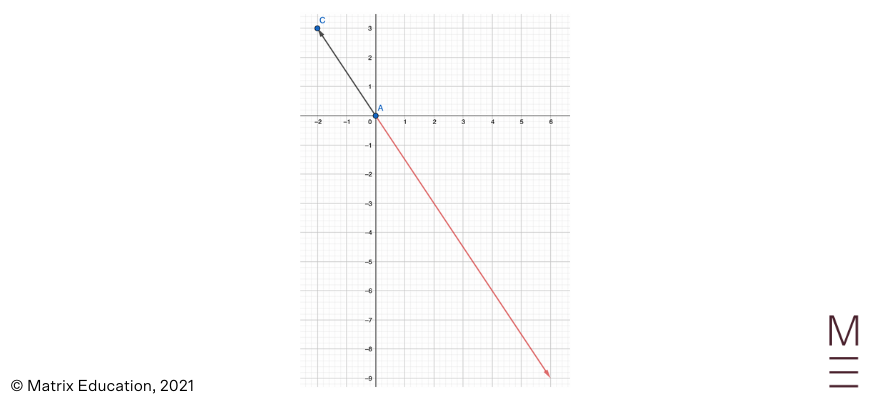
3. \(\frac{1}{4} \vec{AD}\)
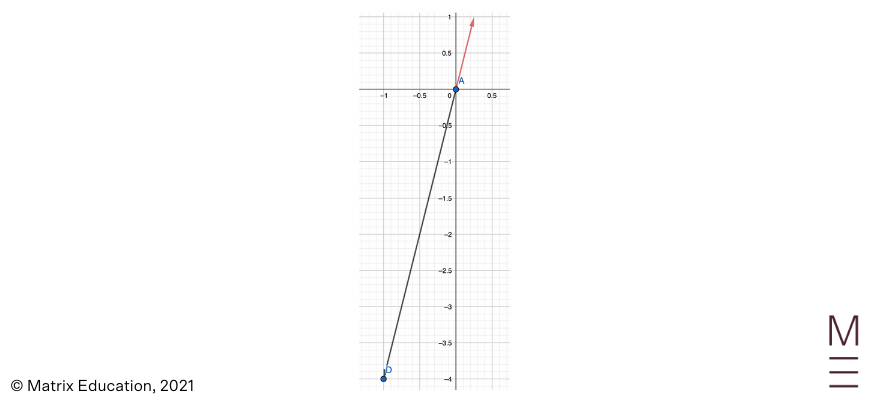
4. \( 2 \vec{AB} + \vec{AC}\)
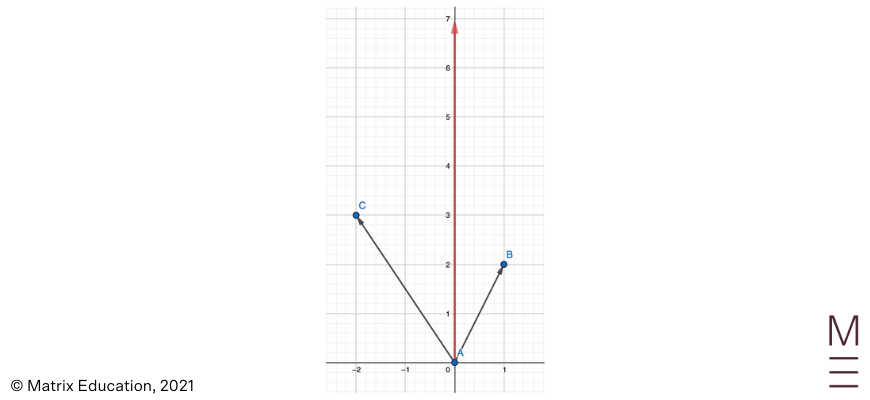
5. \( \frac{1}{2} \vec{AD} – 2\vec{AC}\)
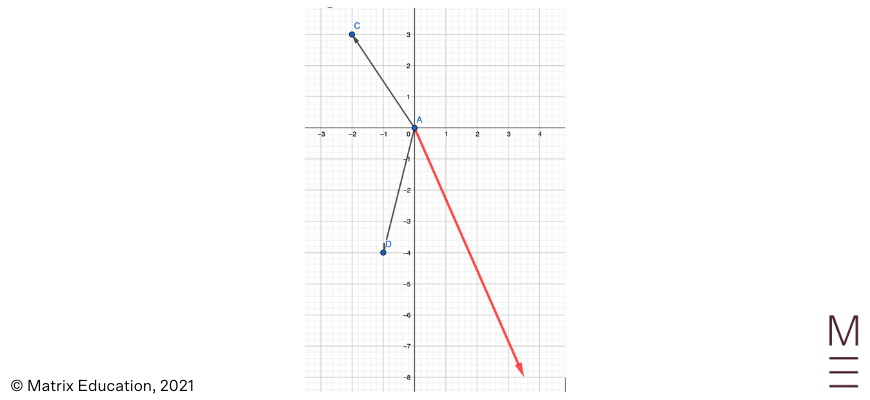
6. \(\frac{1}{2} \vec{AB} – \frac{1}{3} \vec{AC} + 2 \vec{AD}\)
Our Year 12 Maths Ext 1 Course gives you expert teaching, detailed resources, and engaging lessons. Learn more now!
Ace Maths Ext 1 with Matrix+
Expert teachers, weekly quizzes, one-to-one help! Learn at your own pace, wherever you are.
© Matrix Education and www.matrix.edu.au, 2023. Unauthorised use and/or duplication of this material without express and written permission from this site’s author and/or owner is strictly prohibited. Excerpts and links may be used, provided that full and clear credit is given to Matrix Education and www.matrix.edu.au with appropriate and specific direction to the original content.